Building PSL
This page is for building the PSL source code for the purposes of development. For running a standard PSL program, see Running a Program.
To get the code, simply clone the repository:
git clone https://github.com/linqs/psl.gitIf you are already comfortable using Git, then you can just skip ahead to the section on compiling PSL.
Getting started with Git
The Git website has information on installing Git, as does the GitHub guides mentioned below. This tutorial is helpful for learning how to use Git, and this tutorial is particularly helpful for SVN users.
Once Git is installed and you're ready to use it, you can run the above command to clone the PSL repository.
Checking out the development branch
Between releases, the develop branch may be significantly ahead of the master branch. To see the latest changes, checkout the develop branch.
git checkout develop
Contributing Code
To contribute code to PSL first fork the PSL development fork.
Then you clone that repository to a local machine, make commits, and push some or all of those commits back to the repository on GitHub. When your change is ready to be added to PSL, you can submit a pull request which will be reviewed by the PSL maintainers. The maintainers may request that you make additional changes. After your code is deemed acceptable, it will get merged into the develop branch of PSL.
Building PSL
PSL uses the maven build system. Move to the top-level directory of your working copy and run:
mvn compile
You can install PSL to your local Maven repository by running:
mvn install
Updating your pom
Remember to update your project's pom.xml file with the (possibly) new version you installed.
Builtin Similarity Functions
PSL comes with several builtin similarity functions. If you have a need not captured by these functions, then you can also create customized similarity functions.
These similarity functions are shipped with the PSL Utils repository.
Text Similarity
Name: Cosine Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.CosineSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://en.wikipedia.org/wiki/Cosine_similarity
Name: Dice Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.DiceSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://en.wikipedia.org/wiki/S%C3%B8rensen%E2%80%93Dice_coefficient
Name: Jaccard Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.JaccardSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://en.wikipedia.org/wiki/Jaccard_index
Name: Jaro Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.JaroSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://www.census.gov/srd/papers/pdf/rr91-9.pdf
Name: Jaro-Winkler Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.JaroWinklerSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://en.wikipedia.org/wiki/Jaro%E2%80%93Winkler_distance
Name: Level 2 Jaro-Winkler Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.Level2JaroWinklerSimilarity
Arguments: String, String
Return Type: Continuous
Description: A level 2 variation of Jaro-Winkler Similarity. Level 2 means that tokens are broken up before comparison (see http://secondstring.sourceforge.net/javadoc/com/wcohen/ss/Level2.html).
Name: Level 2 Levenshtein Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.Level2LevenshteinSimilarity
Arguments: String, String
Return Type: Continuous
Description: A level 2 variation of Levenshtein Similarity. Level 2 means that tokens are broken up before comparison (see http://secondstring.sourceforge.net/javadoc/com/wcohen/ss/Level2.html).
Name: Level 2 Monge Elkan Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.Level2MongeElkanSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://www.aaai.org/Papers/KDD/1996/KDD96-044.pdf
Name: Levenshtein Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.LevenshteinSimilarity
Arguments: String, String
Return Type: Continuous
Description: https://en.wikipedia.org/wiki/Levenshtein_distance
Name: Same Initials
Qualified Path: org.linqs.psl.utils.textsimilarity.SameInitials
Arguments: String, String
Return Type: Discrete
Description: First splits the input strings on any whitespace and ensures both have the same number of tokens (returns 0 if they do not). Then, the first character of all the tokens are checked for equality (ignoring case and order of appearance). Note that all all character that are not alphabetic ASCII characters are considered equal (eg. all numbers and unicode are considered the same character).
Name: Same Number of Tokens
Qualified Path: org.linqs.psl.utils.textsimilarity.SameNumTokens
Arguments: String, String
Return Type: Discrete
Description: Checks same number of tokens (delimited by any whitespace).
Name: Sub String Similarity
Qualified Path: org.linqs.psl.utils.textsimilarity.SubStringSimilarity
Arguments: String, String
Return Type: Continuous
Description: If one input string is a substring of another, then the length of the substring divided by the length of the text is returned. 0 is returned if neither string is a substring of the other.
CLI Data File Format
The .data files for the PSL CLi are YAML files with some additional constraints.
The accepted top-level keys for data files are:
predicatesobservationstargetstruth
predicates
This section defines the allowed predicates for a PSL program. The minimum amount of information that must be supplied for a predicate is:
- Name
- Arity (how many arguments the predicate has)
- Whether the predicate is
openorclosed.
A simple predicates section may look like:
predicates:
Foo/2: closed
Bar/2: openIn addition to the base information, you can also specify the types of the predicate arguments and whether or not the predicate is a block.
These are specified with the types and block keys respectively.
If the types of a predicate are not explicitly stated, then UniqueStringID is used (or UniqueIntID if --int-ids is specified as a command line option).
If an arity is not specified, then the number of supplied types is inferred to be the arity.
If both the arity and specific types are supplied, then both sizes much match.
Allowed types are specified by the ConstantType enum.
The blocking nature of a predicate is used in some advanced and experimental PSL features.
A more advanced predicates section may look like:
predicates:
Foo/2:
- closed
- types:
- UniqueIntID
- String
Bar:
- open
- types:
- UniqueStringID
- Integer
- blockPartitions
The remaining top level keys are all partitions that data should be loaded into:
observationstargetstruth
In these sections, you specify the files that should be loaded into each partition for each predicate. One or more tab-separated files may be specified for each partition and predicate. If you do not have data for a predicate/partition pairing, just leave it out.
Below is a sample of these sections:
observations:
Foo: foo_obs.txt
Bar: bar_obs.txt
targets:
Foo:
- foo_targets_1.txt
- foo_targets_2.txt
truth:
Foo: foo_truth.txtChange Log
Version 2.1.0 (https://github.com/linqs/psl/tree/2.1.0)
Full Change Information
- PostgreSQL Database Backend
- Removed MySQL support
- Removed the Queries Class
- Removed InserterUtils
- Bulk Dataloading in Postgres
- Deferred Indexing
- No More Predicate Deserialization
- UniqueID Storage Types
- Long Predicate Names Allowed
- CLI Configuration Properties
- Complete CLI Predicate Typing
- Getting the PSL Version
- Random in PSL
- Parallelization in PSL
- Configuration Reworked
- New Canary Naming System
- Inference API Rework
- Moved PSL Evaluation
- Evaluation Infrastructure Changes
- External Function Support
Version 2.0.0 (https://github.com/linqs/psl/tree/2.0.0)
- Add a new type of rule called Arithmetic Rules .
- The use case previously satisfied by Constraints have been replaced by arithmetic rules.
- The Rule Syntax has been expanded to accomodate arithmetic rules.
- Rules in Groovy may now be specified using strings .
- Rules in Groovy may now be specified in bulk using large strings or files.
- A CLI Interface has been added to PSL to help develop program more quickly.
- All PSL packages have been renamed from
edu.umd.cstoorg.linqs. - PSL Examples have been relocated to an external repository instead of a maven archetype.
- Many non-critical components have been moved out to two external repositories:
- The PSL Maven Repository has been moved.
- Bug fixes.
- Performances Enhancements.
Version 1.2.1 (https://github.com/linqs/psl/tree/1.2.1)
- Bug fix for External Function registration
Version 1.2 (https://github.com/linqs/psl/tree/1.2)
- Expectation-maximization and [paired-dual learning] (http://linqs.cs.umd.edu/basilic/web/Publications/2015/bach:icml15/bach-icml15.pdf) in the org.linqs.psl.application.learning.weight.em package
- Topic modeling with latent topic networks in the org.linqs.psl.application.topicmodel package
- Support for averaging rules in the org.linqs.psl.model.kernel.rule package
- New DateTime and Long attribute types in the org.linqs.psl.model.argument package, thanks to Jack Sullivan
- Java 8 compatibility
- Support for MySQL backend (except for external functions)
- Bug fixes
Version 1.1.1 (https://github.com/linqs/psl/tree/1.1.1)
- Improved examples, which demonstrate database population for non-lazy inference and learning
- Support for learning negative weights (limited to inference methods for discrete MRFs that support negative weights)
- Bug fixes
Version 1.1 (https://github.com/linqs/psl/tree/1.1)
- An improved Groovy interface. Try the new examples via https://github.com/linqs/psl/wiki/Installing-examples to learn the new interface.
- New, improved psl-core architecture
- Much faster inference based on the alternating direction method of multipliers (ADMM).
- Improved max-likelihood weight learning
- New max-pseudolikelihood and large-margin weight learning
- Many bug fixes and minor improvements.
Version 1.0.2 (https://github.com/linqs/psl/tree/1.0.2)
- Fixed bugs in HomogeneousIPM and MOSEK add-on caused by bug in parallel colt when using selections from large, sparse matrices.
- Fixed bug when learning weights of programs which contain set functions.
- Reduced memory footprint of HomogeneousIPM and matrices produced by ConicProgram.
Version 1.0.1 (https://github.com/linqs/psl/tree/1.0.1)
- Fixed bug in optimization program when the same atom was used more than once in a ground rule or constraint.
- Added release profile to parent POM for better packaging.
- Minor changes to archetypes.
Version 1.0 (https://github.com/linqs/psl/tree/1.0)
Choosing a Version of PSL
Maven allows several ways to specify acceptable versions for dependencies. This page discusses the recommended options to specifying the PSL version to use.
Exact Version
If you are working on a paper or code that requires exact reproducibility, then you should specify an exact version of PSL.
For example:
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>2.1.3</version>
</dependency>
...
</dependencies>Major Minor
If you want to get bug fixes without worrying about breaking changes, then you can specify a major and minor version while allowing the incremental (patch) version to grow.
For example:
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>[2.1,)</version>
</dependency>
...
</dependencies>Major
If you want the latest stable code and can tolerate the occasional breakage, then you can specify just the major version.
For example:
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>[2,)</version>
</dependency>
...
</dependencies>Canary
If you are doing development any are willing to accept potential bugs, broken builds, and API breakages, then you can use the canary build. See the working with canary page to get detail on how best to work with the canary build.
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>CANARY</version>
</dependency>
...
</dependencies>Configuration Options
Key: admmmemorytermstore.internalstore
Type: String
Default Value: org.linqs.psl.reasoner.term.MemoryTermStore
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.term.ADMMTermStore
Description: Initial size for the memory store.
Key: admmreasoner.epsilonabs
Type: float
Default Value: 1e-5f
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: Absolute error component of stopping criteria. Should be positive.
Key: admmreasoner.epsilonrel
Type: float
Default Value: 1e-3f
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: Relative error component of stopping criteria. Should be positive.
Key: admmreasoner.initialconsensusvalue
Type: String
Default Value: InitialValue.RANDOM.toString()
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: The starting value for consensus variables. Values should come from the InitialValue enum.
Key: admmreasoner.initiallocalvalue
Type: String
Default Value: InitialValue.RANDOM.toString()
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: The starting value for local variables. Values should come from the InitialValue enum.
Key: admmreasoner.maxiterations
Type: int
Default Value: 25000
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: The maximum number of iterations of ADMM to perform in a round of inference.
Key: admmreasoner.objectivebreak
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: Stop if the objective has not changed since the last logging period (see LOG_PERIOD).
Key: admmreasoner.stepsize
Type: float
Default Value: 1.0f
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.ADMMReasoner
Description: Step size. Higher values result in larger steps. Should be positive.
Key: admmtermgenerator.invertnegativeweights
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.reasoner.admm.term.ADMMTermGenerator
Description: If true, then invert negative weight rules into their positive weight counterparts (negate the weight and expression).
Key: arithmeticrule.delim
Type: String
Default Value: ;
Module: psl-core
Defining Class: org.linqs.psl.model.rule.arithmetic.AbstractArithmeticRule
Description: The delimiter to use when building summation substitutions. Make sure the value for this key does not appear in ground atoms that use a summation.
Key: booleanmaxwalksat.maxflips
Type: int
Default Value: 50000
Module: psl-core
Defining Class: org.linqs.psl.reasoner.bool.BooleanMaxWalkSat
Description: Key for positive integer property that is the maximum number of flips to try during optimization
Key: booleanmaxwalksat.noise
Type: double
Default Value: 0.01
Module: psl-core
Defining Class: org.linqs.psl.reasoner.bool.BooleanMaxWalkSat
Description: Key for double property in [0,1] that is the probability of randomly perturbing an atom in a randomly chosen potential
Key: booleanmcsat.numburnin
Type: int
Default Value: 500
Module: psl-core
Defining Class: org.linqs.psl.reasoner.bool.BooleanMCSat
Description: Number of burn-in samples
Key: booleanmcsat.numsamples
Type: int
Default Value: 2500
Module: psl-core
Defining Class: org.linqs.psl.reasoner.bool.BooleanMCSat
Description: Key for length of Markov chain
Key: categoricalevaluator.categoryindexes
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.CategoricalEvaluator
Description: The index of the arguments in the predicate (delimited by colons).
Key: categoricalevaluator.defaultpredicate
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.CategoricalEvaluator
Description: The default predicate to use when none are supplied.
Key: categoricalevaluator.representative
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.CategoricalEvaluator
Description: The representative metric. Default to accuracy. Must match a string from the RepresentativeMetric enum.
Key: continuousevaluator.representative
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.ContinuousEvaluator
Description: The representative metric. Default to MSE. Must match a string from the RepresentativeMetric enum.
Key: continuousrandomgridsearch.maxlocations
Type: int
Default Value: 250
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.ContinuousRandomGridSearch
Description: The max number of locations to search.
Key: discreteevaluator.representative
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.DiscreteEvaluator
Description: The representative metric. Default to F1. Must match a string from the RepresentativeMetric enum.
Key: discreteevaluator.threshold
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.DiscreteEvaluator
Description: The truth threshold.
Key: em.iterations
Type: int
Default Value: 10
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.em.ExpectationMaximization
Description: Key for positive int property for the number of iterations of expectation maximization to perform
Key: em.tolerance
Type: double
Default Value: 1e-3
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.em.ExpectationMaximization
Description: Key for positive double property for the minimum absolute change in weights such that EM is considered converged
Key: executablereasoner.cleanupinput
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.reasoner.ExecutableReasoner
Description: Key for boolean property for whether to delete the input file to external the reasoner on close.
Key: executablereasoner.cleanupoutput
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.reasoner.ExecutableReasoner
Description: Key for boolean property for whether to delete the output file to external the reasoner on close.
Key: executablereasoner.executablepath
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.reasoner.ExecutableReasoner
Description: Key for int property for the path of the executable.
Key: gridsearch.weights
Type: String
Default Value: 0.001:0.01:0.1:1:10
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.GridSearch
Description: A comma-separated list of possible weights. These weights should be in some sorted order.
Key: guidedrandomgridsearch.explorelocations
Type: int
Default Value: 10
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.GuidedRandomGridSearch
Description: The number of initial seed locations to explore based off of whichever ones score the best.
Key: guidedrandomgridsearch.seedlocations
Type: int
Default Value: 25
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.GuidedRandomGridSearch
Description: The number of locations to initially search.
Key: hardem.adagrad
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.em.HardEM
Description: Key for Boolean property that indicates whether to use AdaGrad subgradient scaling, the adaptive subgradient algorithm of John Duchi, Elad Hazan, Yoram Singer (JMLR 2010). If TRUE, will override other step scheduling options (but not scaling).
Key: hyperband.basebracketsize
Type: int
Default Value: 10
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.Hyperband
Description: The base number of weight configurations for each brackets.
Key: hyperband.numbrackets
Type: int
Default Value: 4
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.Hyperband
Description: The number of brackets to consider. This is computed in vanilla Hyperband.
Key: hyperband.survival
Type: int
Default Value: 4
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.Hyperband
Description: The proportion of configs that survive each round in a brancket.
Key: inference.groundrulestore
Type: String
Default Value: org.linqs.psl.application.groundrulestore.MemoryGroundRuleStore
Module: psl-core
Defining Class: org.linqs.psl.application.inference.InferenceApplication
Description: The class to use for ground rule storage.
Key: inference.reasoner
Type: String
Default Value: org.linqs.psl.reasoner.admm.ADMMReasoner
Module: psl-core
Defining Class: org.linqs.psl.application.inference.InferenceApplication
Description: The class to use for a reasoner.
Key: inference.termgenerator
Type: String
Default Value: org.linqs.psl.reasoner.admm.term.ADMMTermGenerator
Module: psl-core
Defining Class: org.linqs.psl.application.inference.InferenceApplication
Description: The class to use for term generator. Should be compatible with REASONER_KEY and TERM_STORE_KEY.
Key: inference.termstore
Type: String
Default Value: org.linqs.psl.reasoner.admm.term.ADMMTermStore
Module: psl-core
Defining Class: org.linqs.psl.application.inference.InferenceApplication
Description: The class to use for term storage. Should be compatible with REASONER_KEY.
Key: initialweighthyperband.internalwla
Type: String
Default Value: MaxLikelihoodMPE.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.InitialWeightHyperband
Description: The internal weight learning application (WLA) to use. Should actually be a VotedPerceptron.
Key: lazyatommanager.activation
Type: double
Default Value: 0.01
Module: psl-core
Defining Class: org.linqs.psl.database.atom.LazyAtomManager
Description: The minimum value an atom must take for it to be activated. Must be a flot in (0,1].
Key: lazymaxlikelihoodmpe.maxgrowrounds
Type: int
Default Value: 100
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.maxlikelihood.LazyMaxLikelihoodMPE
Description: Key for int property for the maximum number of rounds of lazy growing.
Key: lazympeinference.maxrounds
Type: int
Default Value: 100
Module: psl-core
Defining Class: org.linqs.psl.application.inference.LazyMPEInference
Description: Key for int property for the maximum number of rounds of inference.
Key: maxpiecewisepseudolikelihood.numsamples
Type: int
Default Value: 100
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.maxlikelihood.MaxPiecewisePseudoLikelihood
Description: Key for positive integer property. MaxPiecewisePseudoLikelihood will sample this many values to approximate the expectations.
Key: maxspeudolikelihood.bool
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.maxlikelihood.MaxPseudoLikelihood
Description: Boolean property. If true, MaxPseudoLikelihood will treat RandomVariableAtoms as boolean valued. Note that this restricts the types of contraints supported.
Key: maxspeudolikelihood.minwidth
Type: double
Default Value: 1e-2
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.maxlikelihood.MaxPseudoLikelihood
Description: Key for positive double property. Used as minimum width for bounds of integration.
Key: maxspeudolikelihood.numsamples
Type: int
Default Value: 10
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.maxlikelihood.MaxPseudoLikelihood
Description: Key for positive integer property. MaxPseudoLikelihood will sample this many values to approximate the integrals in the marginal computation.
Key: memorytermstore.initialsize
Type: int
Default Value: 5000
Module: psl-core
Defining Class: org.linqs.psl.reasoner.term.MemoryTermStore
Description: Initial size for the memory store.
Key: optimalcover.blockadvantage
Type: double
Default Value: 100.0
Module: psl-core
Defining Class: org.linqs.psl.database.rdbms.OptimalCover
Description: The cost for a blocking predicate is divided by this.
Key: optimalcover.joinadvantage
Type: double
Default Value: 2.0
Module: psl-core
Defining Class: org.linqs.psl.database.rdbms.OptimalCover
Description: The cost for a JOIN.
Key: pairedduallearner.admmsteps
Type: int
Default Value: 1
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.em.PairedDualLearner
Description: Key for Integer property that indicates how many steps of ADMM to run for each inner objective before each gradient iteration (parameter N in the ICML paper)
Key: pairedduallearner.warmuprounds
Type: int
Default Value: 0
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.em.PairedDualLearner
Description: Key for Integer property that indicates how many rounds of paired-dual learning to run before beginning to update the weights (parameter K in the ICML paper)
Key: parallel.numthreads
Type: int
Default Value: Runtime.getRuntime().availableProcessors()
Module: psl-core
Defining Class: org.linqs.psl.util.Parallel
Description:
Key: persistedatommanager.throwaccessexception
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.database.atom.PersistedAtomManager
Description: Whether or not to throw an exception on illegal access. Note that in most cases, this indicates incorrectly formed data. This should only be set to true when the user understands why these exceptions are thrown in the first place and the grounding implications of not having the atom initially in the database.
Key: random.seed
Type: int
Default Value: 4
Module: psl-core
Defining Class: org.linqs.psl.util.RandUtils
Description:
Key: randomgridsearch.maxlocations
Type: int
Default Value: 150
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.RandomGridSearch
Description: The max number of locations to search.
Key: rankingevaluator.representative
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.RankingEvaluator
Description: The representative metric. Default to F1. Must match a string from the RepresentativeMetric enum.
Key: rankingevaluator.threshold
Type:
Default Value:
Module: psl-core
Defining Class: org.linqs.psl.evaluation.statistics.RankingEvaluator
Description: The truth threshold.
Key: ranksearch.scalingfactors
Type: String
Default Value: 1:2:10:100
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.search.grid.RankSearch
Description: A comma-separated list of scaling factors.
Key: rdbmsdatabase.optimalcover
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.database.rdbms.RDBMSDatabase
Description: Use optimal cover grounding.
Key: votedperceptron.averagesteps
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for Boolean property that indicates whether to average all visited weights together for final output.
Key: votedperceptron.clipnegativeweights
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: If true, then weight will not be allowed to go negative (clipped at zero).
Key: votedperceptron.cutobjective
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: If true, then cut the step size in half whenever the objective increases.
Key: votedperceptron.inertia
Type: double
Default Value: 0.00
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: The inertia that is used for adaptive step sizes. Should be in [0, 1).
Key: votedperceptron.l1regularization
Type: double
Default Value: 0.0
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for positive double property scaling the L1 regularization \gamma * |w|
Key: votedperceptron.l2regularization
Type: double
Default Value: 0.0
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for positive double property scaling the L2 regularization (\lambda / 2) * ||w||^2
Key: votedperceptron.numsteps
Type: int
Default Value: 25
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for positive integer property. VotedPerceptron will take this many steps to learn weights.
Key: votedperceptron.scalegradient
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for Boolean property that indicates whether to scale gradient by number of groundings
Key: votedperceptron.scalestepsize
Type: boolean
Default Value: true
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: If true, then scale the step size down by the iteration.
Key: votedperceptron.stepsize
Type: double
Default Value: 0.2
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: Key for positive double property which will be multiplied with the objective gradient to compute a step.
Key: votedperceptron.zeroinitialweights
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.VotedPerceptron
Description: If true, then start all weights at zero for learning.
Key: weightlearning.evaluator
Type: String
Default Value: ContinuousEvaluator.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: An evalautor capable of producing a score for the current weight configuration. Child methods may use this at their own discrection. This is only used for logging/information, and not for gradients.
Key: weightlearning.groundrulestore
Type: String
Default Value: MemoryGroundRuleStore.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: The class to use for ground rule storage.
Key: weightlearning.randomweights
Type: boolean
Default Value: false
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: Randomize weights before running. The randomization will happen during ground model initialization.
Key: weightlearning.reasoner
Type: String
Default Value: ADMMReasoner.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: The class to use for inference.
Key: weightlearning.termgenerator
Type: String
Default Value: ADMMTermGenerator.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: The class to use for term generator. Should be compatible with REASONER_KEY and TERM_STORE_KEY.
Key: weightlearning.termstore
Type: String
Default Value: ADMMTermStore.class.getName()
Module: psl-core
Defining Class: org.linqs.psl.application.learning.weight.WeightLearningApplication
Description: The class to use for term storage. Should be compatible with REASONER_KEY.
Configuration
See the Configuration Options page for all options that PSL uses.
Many components of the PSL software have modifiable parameters and options, called properties.
Every property has a key, which is a string that uniquely identifies it.
These keys are organized into a namespace hierarchy, with each level separated by dots, e.g. <namespace>.<option>.
Each PSL class can specify a namespace for the options used by the class and its subclasses.
For example, the org.linqs.psl.application.learning.weight.VotedPerceptron weight learning class uses the namespace votedperceptron.
Setting the configuration option votedperceptron.stepsize allows you to control the size of the gradient descent update step in the VotedPerceptron weight learning class.
Every property has a type and a default value, which is the value the object will use unless a user overrides it. Every class with properties documents them by declaring their keys as public static final Strings, with Javadoc comments describing the corresponding property's type and semantics. Another public static final member declares the default value for that property.
Setting Properties
Setting properties for PSL programs differ depending on whether you are using the CLI or Java/Groovy interface.
CLI
CLI users can pass any PSL configuration property on the CLI command line.
Just use the -D option and specify the key-value pair.
For example, you can run PSL with debug logging like this:
java -jar psl.jar --infer --data example.data --model example.psl -D log4j.threshold=DEBUGJava/Groovy
PSL projects can specify different configuration bundles in a file named psl.properties on the classpath.
The standard location for this file is <project root>/src/main/resources/psl.properties.
Each key-value pair should be specified on its own line with a <namespace>.<option> = <value> format.
Here is an example psl.properties:
# This is an example properties file for PSL. # # Options are specified in a namespace hierarchy, with levels separated by '.'. # Weight learning parameters # This property specifies the number of iterations of voted perceptron updates votedperceptron.numsteps = 700 # This property specifies the initial step size of the voted perceptron updates votedperceptron.stepsize = 0.1
Getting Properties
Properties can only be fetched from a running program in the Java/Groovy interface.
They are accessed statically via the org.linqs.psl.config.Config class.
For example:
import org.linqs.psl.config.Config;
public static void main(String[] args) {
System.out.println(Config.getString("key", "default"));
}Constraints
Arithmetic rules can be used to enforce modeling constraints. Many different types of constraints can be modeled, this page show a few of the common types.
For these examples, let Foo be the binary predicate that we wish to put constraints on.
(Constraints are not limited to only binary predicates.)
Functional
A Functional constraint enforces the condition that for each possible constant c,
the values of all groundings of Foo(A, c) sum to exactly 1.
Foo(A, +c) = 1 .Note that the rule is unweighted (as indicated by the period at the end).
Inverse Functional
Summing the first argument instead of the second one is often called Inverse Functional. There are no semantic differences between functional and inverse functional constraints.
Foo(+c, A) = 1 .Partial Functional
A Partial Functional constraint is like a functional one, except the value of all groundings of Foo(A, c) sum to 1 or less.
Foo(A, +c) <= 1 .Partial Inverse Functional
Foo(+c, A) <= 1 .Creating a New Project
Before you set up a new project, ensure that the prerequisites are met.
The easiest way to get a new project started in PSL is to copy an existing project. The examples are kept up-to-date and exhibit the preferred style for PSL programs. It is recommended to start there and change the program as you go.
Data Storage in PSL
There are several levels of data abstraction in PSL to help manage and isolate data:
- DataStore
- Database
- Partition
DataStore
The DataStore represents the physical place that all the data is stored. It matches one-to-one with an actual RDBMS database instance (either H2 or PostgreSQL).
All data is stored in tables organized by predicate (one predicate to a table).
Databases are created using their constructor.
In this diagram, you can see how the data resides in the DataStore: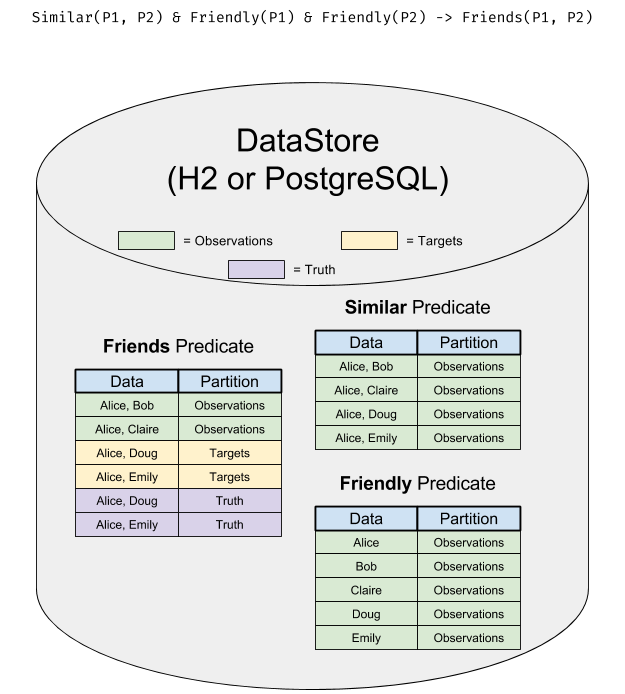
Database
The Database is like a view onto a DataStore where subsets of the data are assigned to be read/write, read-only, or inaccessible. This makes it easy to do things like have observations and truth in the same database without worrying about one leaking into the other.
To get a database, you call DataStore.getDatabase on a DataStore.getDatabase() takes two required arguments and one variadic argument:
- The write partition (this partition will be marked as read/write).
- A set of predicates to be considered "closed".
- Any number of read partition (these partitions will all be marked as read-only).
In this diagram, you can see what a Database set up for inference looks like: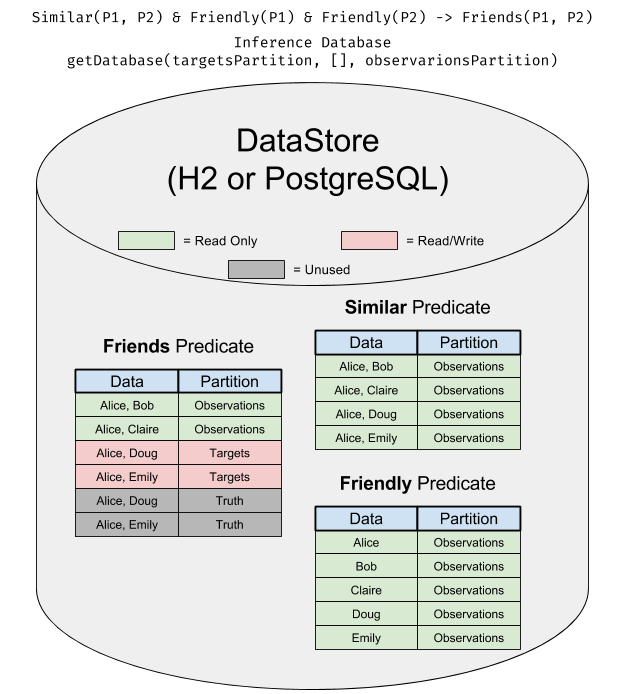
In this diagram, you can see what a Database set up as a truth for weight learning or evaluation looks like: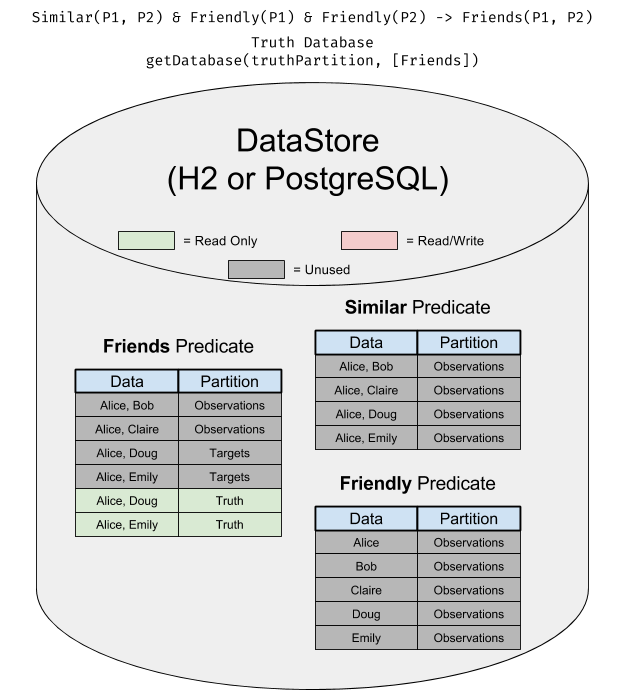
Partition
A Partition is the most fine-grained collection of data in PSL. Every ground atom (piece of data) belongs to exactly one partition. Within a partition, all data must be unique (an exception will be thrown during data loading if this is broken).
In most cases, you will want two or three partitions for inference:
observations- for observed data that has a fixed value.targets- for the data you want to infer.truth- optional truth values for that targets that you can use for evaluation.
Development Coding Style
Follow the Google style guide with the following exceptions:
- Non static imports are separated into in three blocks (in this order):
- Classes within the PSL project (including utils/experimental).
- Third party classes not part of the Java standard library.
- Java standard library classes.
- Indentation is 4 spaces.
- Hard tabs. (But this will change to soft tabs in the near future.)
- Consecutive blank lines are not allowed.
- Avoid block comments (
/* */) inside methods. - Don't use
@authortags in javadoc comments.
Eclipse integration
Since PSL is built with Java and Maven, many IDEs are supported. (Although many PSL developers prefer using vim/emacs and a terminal.) One of the popular supported IDEs is Eclipse.
Eclipse is an extensible, integrated development environment that can be used to develop PSL and PSL projects. The recommended way of using Eclipse with PSL is to use the Eclipse plugin for Maven to generate Eclipse project information for a PSL project and then import that project into Eclipse.
Prerequisites
Ensure that you have version 3.6 (Helios) or higher of Eclipse installed. Then, install the Groovy Eclipse plugin and the optional 1.8 version of the Groovy compiler, which is available when installing the plugin. The version 1.8 compiler is what Maven will use to compile the Groovy scripts, so builds done by either tool should be interchangeable. If you use an older version, Eclipse will probably recompile some files which then won't be compatible with the rest, and it won't run. (Cleaning and rebuilding everything should help.)
You might have to change the Groovy compiler version to 1.8.x in your Groovy compiler preferences (part of the Eclipse preferences).
You need to add a classpath variable in Eclipse to point to your local Maven repository.
You can access the variables either from the main options or from the build-path editor for any project.
Where you specify additional libs, make a new variable (there should be a button) with the name M2_REPO and the path to your repo (e.g., ~/.m2/repository).
This can also be achieved automatically via the following Maven command:
mvn -Declipse.workspace=/path/to/workspace eclipse:configure-workspace
Generating and importing Eclipse metadata
In the top-level directory of your PSL project, run:
mvn eclipse:eclipse
Then in Eclipse, go to File/Import/General/\<something like 'Existing Project'\>.
Select the top-level directory of your project.
You probably don't want to copy it into the workspace, so uncheck that option.
Running programs
Be sure to run as a "Java application."
Tips
If you want to delete the Eclipse metadata for any reason, run:
mvn eclipse:cleanIf you want to generate metadata for a project that depends on another project you're developing with Eclipse (PSL or not), run:
mvn eclipse:eclipse -Declipse.workspace=<path to Eclipse workspace>The Eclipse plugin for Maven will look in the provided workspace for any projects that match dependencies declared in your project's POM file. Your project will be configured to depend on any such projects found as opposed to their respective installed jars. This way, changes to the sources of those dependencies will be seen by your project without reinstalling the dependencies. Note that this works even for dependencies that were imported but not copied into the workspace.
The m2eclipse Eclipse plugin is another option for developing PSL projects with Eclipse. It differs from the recommended method in that it is an Eclipse plugin designed to support Maven projects, as opposed to a Maven plugin designed to support Eclipse.
Example Walkthrough
This page will walk you through the Groovy version of the Simple Acquaintances example.
Setup
First, ensure that your system meets the prerequisites .
Then clone the psl-examples repository:
git clone https://github.com/linqs/psl-examples.gitRunning
Then move into the root directory for the simple acquaintances groovy example:
cd psl-examples/simple-acquaintances/groovyEach example comes with a run.sh script to quickly compile and run the example.
To compile and run the example:
./run.shTo see the output of the example, check the inferred-predicates/KNOWS.txt file:
cat inferred-predicates/KNOWS.txtYou should see some output like:
'Arti' 'Ben' 0.48425865173339844
'Arti' 'Steve' 0.5642937421798706
< ... 48 rows omitted for brevity ...>
'Jay' 'Dhanya' 0.4534565508365631
'Alex' 'Dhanya' 0.48786869645118713The exact order of the output may change and some rows were left out for brevity.
Now that we have the example running, lets take a look inside the only source file for the example:
src/main/java/org/linqs/psl/examples/simpleacquaintances/Run.groovy.
Configuration
All configuration in PSL is handled through the Config object.
By default, PSL will look for two configuration files: psl.properties and log4j.properties.
You can find these files in the src/main/resources directory.
The Config class will automatically load these files (if they exist) and all the options in them.
Configuration options can still be set using the addProperty() and setProperty() methods of the Config class.
Defining Predicates
The definePredicates() method defines the three predicates for our example:
model.add predicate: "Lived", types: [ConstantType.UniqueStringID, ConstantType.UniqueStringID];
model.add predicate: "Likes", types: [ConstantType.UniqueStringID, ConstantType.UniqueStringID];
model.add predicate: "Knows", types: [ConstantType.UniqueStringID, ConstantType.UniqueStringID];Each predicate here takes two unique string identifiers as arguments.
Note that for unique identifiers, ConstantType.UniqueStringID and ConstantType.UniqueIntID are available.
Having integer identifiers usually requires more pre-processing on the user's side, but gains better performance.
- Lived indicates that a person has lived in a specific location. For example: Lived(Sammy, SantaCruz) would indicate that Sammy has lived in Santa Cruz.
- Likes indicates the extent to which a person likes something. For example: Likes(Sammy, Hiking) would indicate the extent that Sammy likes hiking.
- Knows indicates that a person knows some other person. For example: Knows(Sammy, Jay) would indicate that Sammy and Jay know each other.
Defining Rules
The defineRules() method defines six rules for the example.
There are pages that cover the PSL rule specification and the rule specification in Groovy .
We will discuss the following two rules:
model.add(
rule: "20: Lived(P1, L) & Lived(P2, L) & (P1 != P2) -> Knows(P1, P2) ^2"
);
model.add(
rule: "5: !Knows(P1, P2) ^2"
);The first first rule can be read as "If P1 and P2 are different people and have both lived in the same location, L, then they know each other". Some key points to note from this rule are:
- The variable
Lwas reused in bothLivedatoms and therefore must refer to the same location. (P1 != P2)is shorthand for P1 and P2 referring to different people (different unique ids).
The second rule is a special rule that acts as a prior. Notice how this rule is not an implication like all the other rules. Instead, this rule can be read as "By default, people do not know each other". Therefore, the program will start with the belief that no one knows each other and this prior belief will be overcome with evidence.
Loading Data
The loadData() method loads the data from the flat files in the data directory into the data store that PSL is working with.
For berevity, we will only be looking at two files:
Inserter inserter = dataStore.getInserter(Lived, obsPartition);
inserter.loadDelimitedData(Paths.get(DATA_PATH, "lived_obs.txt").toString());
inserter = dataStore.getInserter(Likes, obsPartition);
inserter.loadDelimitedDataTruth(Paths.get(DATA_PATH, "likes_obs.txt").toString());Both portions load data using an Inserter.
The primary difference between the two calls is that the second one is looking for a truth value while the first one assumes that 1 is the truth value.
If we look in the files, we see lines like:
../data/lives_obs.txt
Jay Maryland
Jay California../data/likes_obs.txt
Jay Machine Learning 1
Jay Skeeball 0.8In lives_obs.txt, there is no need to use a truth value because living somewhere is a discrete act.
You have either lived there or you have not.
Liking something, however, is more continuous.
Jay may like Machine Learning 100%, but he only likes Skeeball 80%.
Partitions
Here we must take a moment to talk about data partitions. In PSL, we use partitions to organize data. A partition is nothing more than a container for data, but we use them to keep specific chunks of data together or separate. For example if we are running evaluation, we must be sure not use our test partition in training. A more complete discussion of partitions and data storage in PSL can be found here on this page .
PSL users typically organize their data in at least three different partitions (all of which you can see in this example):
- observations (called
obsPartitionin this example): In this partition we put actual observed data. In this example, we put all the observations about who has lived where, who likes what, and who knows who in the observations partition. - targets (called
targetsPartitionin this example): In this partition we put atoms that we want to infer values for. For example if we want to if Jay and Sammy know each other, then we would put the atomKnows(Jay, Sammy)into the targets partition. - truth (called
truthPartitionin this example): In this partition we put our test set, data that we have actual values for but are not including in our observations for the purpose of evaluation. For example, if we know that Jay and Sammy actually do know each other, we would putKnows(Jay, Sammy)in the truth partition with a truth value of 1.
Running Inference
The runInference() method handles running inference for all the data we have loaded.
Before we run inference, we have to set up a database to use for inference:
Database inferDB = dataStore.getDatabase(targetsPartition, [Lived, Likes] as Set, obsPartition);The getDatabase() method of DataStore is the proper way to get a database.
This method takes a minimum of two parameters:
- The partition that this database is allowed to write to. In inference, we will be writing the inferred truth values of atom to the target partition, so we will need to have it open for writing.
- A set of partitions to be closed in the write partition. Even though we are writing values into the write partition, we may only have a few predicates that we actually want to infer values for. This parameter allows you to close those predicates that you do not what changed.
Lastly,
getDatabase()takes any number of read-only partitions that you want to include in this database. In our example, we want to include our observations when we run inference.
Now we are ready to run inference:
InferenceApplication inference = new MPEInference(model, inferDB);
inference.inference();
inference.close();
inferDB.close();To the MPEInference constructor, we supply our model and the database to infer over.
To see the results, then we will need to look inside of the target partition.
Output
The method writeOutput() handles printing out the results of the inference.
There are two key lines in this method:
Database resultsDB = ds.getDatabase(targetsPartition);
...
for (GroundAtom atom : resultsDB.getAllGrondAtoms(Knows)) {The first line gets a fresh database that we can get the atoms from.
Notice that we are passing in targetsPartition as a write partition, but we are actually just reading from it.
The second line uses the Queries class to iterate over all the Knows atoms from the database we just created.
Evaluation
Lastly, the evalResults() method handles seeing how well our model did.
The DiscreteEvaluator class provides basic tools to compare two partitions.
In this example, we are comparing our target partition to our truth partition.
Examples
Example PSL programs are available at https://github.com/linqs/psl-examples.
Each example contains a script called run.sh which will handle all the building and running.
A detailed walkthrough of an example can he found here .
External Functions
Customized functions can be created be implementing the ExternalFunction interface.
The getValue() method should return a value in [0, 1].
public class MyStringSimilarity implements ExternalFunction {
@Override
public int getArity() {
return 2;
}
@Override
public ConstantType[] getArgumentTypes() {
return [ConstantType.String, ConstantType.String].toArray();
}
@Override
public double getValue(ReadableDatabase db, Constant... args) {
return args[0].toString().equals(args[1].toString()) ? 1.0 : 0.0;
}
}A function comparing the similarity between two entities or text can then be declared as follows:
model.add function: "MyStringSimilarity", implementation: new MyStringSimilarity();A function can be used in the same manner as a predicate in rules:
Name(P1, N1) & Name(P2, N2) & MyStringSimilarity(N1, N2) -> SamePerson(P1, P2)
Glossary
The PSL software uses concepts from the core PSL paper, and introduces new ones for advanced data management and machine learning. On this page, we define the commonly used terms and point out the corresponding classes in the code base.
Please note that this page is organized conceptually, not alphabetically.
Preliminaries
Hinge-loss Markov random field: A factor graph defined over continuous variables in the [0,1] interval with (log) factors that are hinge-loss functions. Many classes in PSL work together to implement the functionality of HL-MRFs.
Ground atom:
A logical relationship corresponding to a random variable in a HL-MRF.
For example, Friends("Steve", "Jay") is an alias for a specific random variable.
Random variable atom: A ground atom that is unobserved, i.e., no value is known for it. A HL-MRF assigns probability densities to assignments to random variable atoms.
Observed atom: A ground atom that has an observed, immutable value. HL-MRFs are conditioned on observed atoms.
Atom:
A generalization of ground atoms that allow logical variables as placeholders for constant arguments.
For example, Friends("Steve", A) is a placeholder for all the ground atoms that can be obtained by substituting constants for the logical variable A.
Syntax
PSL Program: A set of rules, each of which is a template for hinge-loss potentials or hard linear constraints. When grounded over a base of ground atoms, a PSL program induces a HL-MRF conditioned on any specified observations.
Rule: See Rule Specification .
Data Management
See this page for more details.
Data Store: An entire data repository, such as a relational database management system (RDBMS).
Partition: A logical division of ground atoms in a data store.
Database: A logical view of a data store, constructed by specifying a write partition and one or more read partitions of a data store.
Open Predicate: A predicate whose atoms can be random variable atoms, i.e., unobserved. The only time a ground atom will be loaded as a random variable atom is when it is stored in the database's write partition and its predicate is not specified as closed. Otherwise it will be loaded as an observed atom. Whether a predicate is open or closed is specific to each database.
Closed Predicate: A predicate whose atoms are always observed atoms. The only time a ground atom will be loaded as a random variable atom is when it is stored in the database's write partition and its predicate is not specified as closed. Otherwise it will be loaded as an observed atom. Whether a predicate is open or closed is specific to each database.
H2 Web Interface
If you use H2 as the backend database for PSL (as is done in the examples), it can be helpful to open up the resulting database and examine it for debugging purposes.
Prerequisites
You should set up your PSL program to use H2 on disk and note where it is stored. For example, if you create your DataStore using the following code
DataStore data = new RDBMSDataStore(new H2DatabaseDriver(Type.Disk, "/home/bob/psl", true));then PSL will create an H2 database in the file /home/bob/psl/psl.mv.db.
Then, run your program so the resulting H2 database can be inspected.
Starting the H2 Web Server
You will need to use the H2 jar for your classpath. This is likely ~/.m2/repository/com/h2database/h2/1.4.192/h2-1.4.192.jar, but you may need to modify it if, for example, you're using a different version of H2.
You start the H2 web server by running the following command:
java -cp ~/.m2/repository/com/h2database/h2/1.4.192/h2-1.4.192.jar org.h2.tools.ServerUsing the H2 Web Server
Once you have started the web server, you can access it at http://localhost:8082.
To log in, you should change the connection string to point to your H2 database file without .mv.db on the end. The username and password are both empty strings.
Home
Welcome to the PSL software Wiki!
Getting Started with Probabilistic Soft Logic
To get started with PSL you can follow one of these guides:
Command Line Interface for New Users : The Command Line Interface (CLI) will be sufficient for most use cases and we recommend that all users start with it. It is the easiest way to get started with PSL. If you need to take advantage of more advanced / low-level PSL features, then you can move to the Groovy interface.
Groovy for Intermediate Users : If you are comfortable with Java/Groovy and need to take advantage of more advanced / low-level PSL features, then we recommend that you use our Groovy interface.
PSL requires Java, so before you start make sure that you have Java installed.
Learning More About PSL
Probabilistic soft logic (PSL) is a machine learning framework for developing probabilistic models. PSL models are easy to use and fast. You can define models using a straightforward logical syntax and solve them with fast convex optimization. PSL has produced state-of-the-art results in many areas spanning natural language processing, social-network analysis, knowledge graphs, recommender system, and computational biology.
Resources
Introduction to Probabilistic Soft Logic
Probabilistic soft logic (PSL) is a general purpose language for modeling probabilistic and relational domains. It is applicable to a variety of machine learning problems, such as link prediction and ontology alignment. PSL combines the strengths of two powerful theories -- first-order logic, with its ability to succinctly represent complex phenomena, and probabilistic graphical models, which capture the uncertainty and incompleteness inherent in real-world knowledge. More specifically, PSL uses "soft" logic as its logical component and Markov random fields as its statistical model.
In "soft" logic, logical constructs need not be strictly false (0) or true (1),
but can take on values between 0 and 1 inclusively.
For example, in logical formula similarNames(X, Y) => sameEntity(X, Y)
(which encodes the belief that if two people X and Y have similar names, then they are likely the same person),
the truth value of similarNames(X, Y) and that of the entire formula lie in the range [0, 1].
The logical operators and (^), or (v) and not (~) are defined using the Lukasiewicz t-norms, i.e.,
A ^ B = max{A + B - 1, 0}
A v B = min{A + B, 1}
~A = 1 - A(Note that if the values of A and B are restricted to be false or true, then the logical operators work as they are conventionally defined.)
These logical formulas become the features of a Markov network. Each feature in the network is associated with a weight, which determines its importance in the interactions between features. Weights can be specified manually or learned from evidence data using PSL's suite of learning algorithms. PSL also provides sophisticated inference techniques for finding the most likely answer (i.e. the MAP state) to a user's query. The "softening" of the logical formulas allows us to cast the inference problem as a polynomial-time optimization, rather than a (much more difficult NP-hard) combinatorial one. (See LP relaxation for more details.)
For more details on PSL, please refer to the paper Hinge-Loss Markov Random Fields and Probabilistic Soft Logic.
Logging
PSL uses SLF4J for logging.
Java/Groovy
In the PSL Groovy program template, SLF4J is bound to Log4j 1.2.
The Log4j configuration file is located at src/main/resources/log4j.properties.
It should look something like this:
# Set root logger level to the designated level and its only appender to A1.
log4j.rootLogger=INFO, A1
# A1 is set to be a ConsoleAppender.
log4j.appender.A1=org.apache.log4j.ConsoleAppender
# A1 uses PatternLayout.
log4j.appender.A1.layout=org.apache.log4j.PatternLayout
log4j.appender.A1.layout.ConversionPattern=%-4r [%t] %-5p %c %x - %m%n
# Change our connection pool to only log errors.
# Since we may set our root logger to something more loose, we want to explicitly set this.
org.slf4j.simpleLogger.log.com.zaxxer.hikari=ERROR
log4j.logger.com.zaxxer.hikari=ERRORThe logging verbosity can be set by changing ERROR in the second line to a different level and recompiling. Options include OFF, WARN, DEBUG, and TRACE.
CLI
In the command line interface, the logging level can be set using the same logging levels like this:
java -jar psl.jar --infer --data example.data --model example.psl -D log4j.threshold=DEBUGMOSEK add on
MOSEK is software for numeric optimization. PSL can use MOSEK as a conic program solver via a PSL add on. Mosek support is provided as part of the PSL Experimental package.
Setting up the MOSEK add on
First, install MOSEK 6.
In addition to a commercial version for which a 30-day trial is currently available, the makers of MOSEK also currently offer a free academic license.
Users will need the "PTS" base system for using the linear distribution of the ConicReasoner and the "PTON" non-linear and conic extension to use the quadratic distribution.
Both of these components are currently covered by the academic license.
After installing MOSEK, install the included mosek.jar file to your local Maven repository. (This file should be in <mosek-root>/6/tools/platform/<your-platform>/bin.)
mvn install:install-file -Dfile=<path-to-mosek.jar> -DgroupId=com.mosek \
-DartifactId=mosek -Dversion=6.0 -Dpackaging=jarNext, add the following dependency to your project's pom.xml file:
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-mosek</artifactId>
<version>YOUR-PSL-VERSION</version>
</dependency>
...
</dependencies>where YOUR-PSL-VERSION is replaced with your PSL version.
Finally, it might be necessary to rebuild your project:
mvn clean compile
Using the MOSEK add on
After installing the MOSEK add on, you can use it where ever a ConicProgramSolver is used.
To use it for inference with a ConicReasoner set the conicreasoner.conicprogramsolver configuration property to oorg.linqs.psl.optimizer.conic.mosek.MOSEKFactory.
Further, MOSEK requires that two environment variables be set when running.
The same bin directory where you found mosek.jar needs to be on the path for shared libraries.
The environment variable MOSEKLM_LICENSE_FILE needs to be set to the path to your license file (usually <mosek-root>/6/licenses/mosek.lic).
In bash in Linux, this can be done with the commands
export LD_LIBRARY_PATH=<path_to_mosek_installation>/mosek/6/tools/platform/<platform>/bin
export MOSEKLM_LICENSE_FILE=<path_to_mosek_installation>/mosek/6/licenses/mosek.licOn Mac OS X, instead set DYLD_LIBRARY_PATH to the directory containing the MOSEK binaries.
Migrating to PSL 2
Maven Repository Move
Our Maven repository has moved
- from:
https://scm.umiacs.umd.edu/maven/lccd/content/repositories/psl-releases/ - to:
http://maven.linqs.org/maven/repositories/psl-releases/
The new endpoint will redirect to a https endpoint that may be used if necessary:
https://linqs-data.soe.ucsc.edu/maven/repositories/psl-releases/
Naming Changes
Package Renames
All packages have been renamed from edu.umd.cs.* to org.linqs.*.
Renames/Moves
edu.umd.cs.psl.model.argument.ArgumentType→org.linqs.psl.model.term.ConstantType
Usage Changes
Predicate Arguments
ArgumentType.* → ConstantType.*
The arguments for a predicate are now defined in org.linqs.psl.model.term.ConstantType instead of edu.umd.cs.psl.model.argument.ArgumentType.
All the same types are supported, just the containing class has been moved and renamed.
Getting a Partition
new Partition(int) → DataStore.getPartition("stringIdentifier")
If the partition does not exist, it will be created and returned.
If it exists, it will be returned.
It is not longer necessary to pass around partitions if you don't want to.
Changes to Rule Syntax
Arithmetic rules are now supported in 2.0. See the Rule Specification for details. Rules in Groovy can now be specified in additional ways. See Rule Specification in Groovy .
Constraints
Constraints are now implemented using unweighted arithmetic rules. See Constraints for more details.
Util and Experimental Breakout
To speed up utility development and reduce bloat, some components have been removed from this primary PSL repository and brought into their own repositories.
In these sample POM snippets all versions have been set to CANARY, however you may choose your corresponding release.
PSL Utils
https://github.com/linqs/psl-utils
Data Loading - psl-dataloading
Maven Dependency Declaration
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-dataloading</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.ui.loadingedu.umd.cs.psl.ui.data
New Package
org.linqs.psl.utils.dataloading
Evaluation - psl-evaluation
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-evaluation</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.evaluation
New Package
org.linqs.psl.utils.evaluation
Text Similarity - psl-textsim
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-textsim</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.ui.functions.textsimilarity
New Package
org.linqs.psl.utils.textsimilarity
PSL Experimental
https://github.com/linqs/psl-experimental
Data Splitter - psl-datasplitter
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-datasplitter</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.util.datasplitter
New Package
org.linqs.psl.experimental.datasplitter
Experiment - psl-experiment
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-experiment</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.ui.experiment
New Package
org.linqs.psl.experimental.experiment
Mosek - psl-mosek
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-mosek</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.optimizer.conic.mosek
New Package
org.linqs.psl.optimizer.conic.mosek
Optimize - psl-optimize
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-optimize</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.optimizeredu.umd.cs.psl.reasoner.conic
New Package
org.linqs.psl.experimental.optimizer
Sampler - psl-sampler
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-sampler</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.sampler
New Package
org.linqs.psl.experimental.sampler
Weight Learning - psl-weightlearning
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-weightlearning</artifactId>
<version>CANARY</version>
</dependency>Included (Old) Packages
edu.umd.cs.psl.application.learning.weight.maxmargin
New Package
org.linqs.psl.experimental.learning.weight.maxmargin
Prerequisites
The following software is required to use PSL:
Java 7 or 8 JDK
Ensure that the Java 7 or 8 development kit is installed. Either OpenJDK or Oracle Java work.
We have had some reports of failing builds using Java prior to 1.7.0_110 or 1.8.0_110.
If you have issues with Maven (especially handshake errors), try updating your version of java to at least 1.7.0_110 or 1.8.0_110.
This is especially relevant for Mac users where the version of Java is less frequently updated.
Maven 3.x
PSL uses Maven to manage builds and dependencies. Users should install Maven 3.x. PSL is developed with Maven and PSL programs are created as Maven projects. See running Maven for help using Maven to build projects.
Rule Specification in Groovy
Models in Groovy support three different ways to specify rules:
In-Line Syntax
Rules can be specified using the natural Groovy syntax and the add() method for models. The rule weight and squaring must be specified as additional arguments. Both may be left off to specify an unweighted rule.
model.add(
rule: ( Likes(A, 'Dogs') & Likes(B, 'Dogs') ) >> Friends(A, B),
weight: 5.0,
squared: true
);Because the in-line syntax must be a subset of Groovy syntax, the following operator variants are not supported:
&&||-><<<-!
Note that there are supported variants for all unsupported operators. Arithmetic rules are not supported with the in-line syntax.
String Syntax
model.add(
rule: "( Likes(A, 'Dogs') & Likes(B, 'Dogs') ) >> Friends(A, B)",
weight: 5.0,
squared: true
);
// Produces the same rule as above.
model.add(
rule: "5.0: ( Likes(A, 'Dogs') && Likes(B, 'Dogs') ) -> Friends(A, B) ^2"
);
// An unweighted (constraint) variant of the above rule.
model.add(
rule: "( Likes(A, 'Dogs') && Likes(B, 'Dogs') ) -> Friends(A, B)"
);
// An arithmetic constraint.
model.add(
rule: "Likes(A, +B) = 1 ."
);Rules can also be specified directly as a string. Because they are not limited by the Groovy syntax, all operators are available. A rule that specifies a weight and squaring in the string may not also pass "weight" and "squared" arguments.
Bulk String Syntax
// Load multiple rules from a single string.
model.addRules("""
1: ( Likes(A, 'Dogs') & Likes(B, 'Dogs') ) >> Friends(A, B) ^2
Likes(A, +B) = 1 .
""");
// Load multiple rules from a file.
model.addRules(new FileReader("myRules.txt"));The addRules() method may be used add multiple rules at a time, each rule on its own line.
A String or Reader may be passed.
Each rule must be fully specified with respects to weights and squaring.
Constraints
Constraints are specified as unweighted arithmetic rules. So all you need to do is make an arithmetic rule and either explicitly specify that it is unweighted (using the period syntax), or not specify a weight.
`groovy
// An unweighted rule (constraint) explicitly specified with a period.
model.add(
rule: "Likes(A, +B) = 1 ."
);
// An unweighted rule (constraint) implicitly specified by not adding a weight. model.add( rule: "Likes(A, +B) = 1" );
Rule Specification
PSL supports two primary types of rules: Logical and Arithmetic. Each of these types of rules support weights and squaring.
Logical Rules
Logical rules in PSL are implications joined with logical operators (with the exception of negative priors). Since PSL uses soft logic, hard logic operators are replaced with Lukasiewicz operators.
Operators
& (&&) - Logical And
The and operator is binary and functions as a Lukasiewicz t-norm operator:
A & B = MAX(0, A + B - 1)
| (||) - Logical Or
The or operator is binary and functions as a Lukasiewicz t-conorm operator:
A | B = MIN(1, A + B)
>> (->) / << (<-) - Implication
The implication operator acts similar to the standard logical implication where the truth of the body implies the truth of the head.
Note that the head is always the side the that arrow is pointing at and both directions are supported.
It is most common to see rules where the body is on the left and the head is on the right.
The body of an implication must be a conjunctive clause (contain only and operators) while the head must be a disjunctive clause (contain only or operators).
~ (!) - Negation
The negation operator is unary and functions as a Lukasiewicz negation operator:
~A = 1 - A
Examples
// The same rule written in two different ways.
Nice(A) & Nice(B) -> Friends(A, B)
Friends(A, B) << Nice(A) && Nice(B)
// Using a disjunction in the head instead of a conjunction in the body.
// Also written two different ways.
Friends(A, B) >> Nice(A) || Nice(B)
Nice(A) | Nice(B) <- Friends(A, B)Arithmetic Rules
Arithmetic rules are relations of two linear combinations.
Operators
The following operators are used in arithmetic rules:
+-*/
Note that each side of an arithmetic rule must be a linear combination, so +/- is only allowed between terms and *// is only allowed for coefficients.
Relational Operator
The following relational operators are allowed between the two linear combinations:
=<=>=
Summation
A summation can be used when you want to aggregate over a variable.
You turn a variable into a summation variable by prefixing it with a +.
Each sum variable can only be used once per expression, but you may have multiple different summation variables.
Filter Clauses
A filter clause appears at the end of a rule and decides what values the summation variable can take. There can be multiple filter clauses for each rule, but each summation variable can have at most one filter clause. The filter clause is a logical expression, but uses hard logic rather than Lukasiewicz. All non-zero truth values are considered true in a filter expression. If this expression evaluates to zero for a value, then that value is not used in the summation. Valid things that may appear in the filter clause are:
- Constants
- Variables appearing in the associated arithmetic expression
- Closed predicates
- The single summation variable that was defined as the argument
// Only sum up friends of A that are nice.
Friends(A, +B) <= 1 {B: Nice(B)}
// Only sum up friends of A that are similar to A.
// Note that Similar must be a closed predicate.
Friends(A, +B) <= 1 {B: Similar(A, B)}
// Only sum up friends of A that are not similar to A.
// Note that Similar must be a closed predicate.
Friends(A, +B) <= 1 {B: !Similar(A, B)}
// Only sum up friends of A where both A and B are nice and similar.
// Note that Similar must be a closed predicate.
Friends(A, +B) <= 1 {B: Nice(A) & Nice(B) & Similar(A, B)}
// Only sum up combinations for friends where A is nice and B is not nice.
Friends(+A, +B) <= 1 {A: Nice(A)} {B: !Nice(B)}Coefficients
Each term in an arithmetic rule can take an optional coefficient. The coefficient may be any real number and can either appear before the term and act as a multiplier:
2.5 * Similar(A, B) >= 1or, appear after the term and act as a divisor:
Similar(A, B) / 2.5 <= 1Coefficient Operators
Special coefficients (called Coefficient Operators) may be used:
|A| - Cardinality
A cardinality coefficient may only be used on a summation variable.
It becomes the count of the number of terms substituted for a summation variable.
@Min[A, B] - Max
Returns the maximum of A and B.
May be used with summation variables.
@Max[A, B] - Min
Returns the minimum of A and B.
May be used with summation variables.
Examples
(Note that these rules are meant to show the semantics of arithmetic rules and may not make logical sense.)
Friends(A, B) = 0.5
Friends(A, +B) <= 1
Friends(A, +B) / |B| <= 1
@Min[2, |B|] * Friends(A, +B) <= 1
Friends(A, +B) <= 1 {B: Nice(B)}
Friends(A, B) <= Nice(A) + Nice(B)
Friends(A, B) >= 3.0 * Nice(A) - 2.0 * Nice(B)Weights
Every rule must be either weighted or unweighted. Unweighted rules are also called constraints since they are strictly enforced.
Weighted
Weighted rules are prefixed with the weight and a colon:
<weight>: <rule>For example:
2.5: Nice(A) & Nice(B) & (A != B) -> Friends(A, B)
5.0: Friends(A, +B) <= 1
10.0: Friends(A, +B) <= 1 {B: Nice(B)}Unweighted
Unweighted rules are suffixed with a period:
<rule> .For example:
Nice(A) & Nice(B) & (A != B) -> Friends(A, B) .
Friends(A, +B) <= 1 .
Friends(A, +B) <= 1 . {B: Nice(B)}Squaring
Any weighted rule can choose to square their hinge-loss functions.
Squaring the hinge-loss (or "squared potentials") may result in better performance.
Non-squared potentials tend to encourage a "winner take all" optimization, while squared potentials encourage more trading off.
To square a rule, just suffix a ^2 to it:
2.5: Nice(A) & Nice(B) (A != B) -> Friends(A, B) ^2
5.0: Friends(A, +B) <= 1 ^2
10.0: Friends(A, +B) <= 1 ^2 {B: Nice(B)}Priors
You may specify priors for a predicate in PSL. A prior is specified on a specific predicate and affects all open ground atoms of that predicate. Priors in PSL must be weighted and may be squared. Priors tend to have low weights, since they are supposed to get overpowered by evidence.
Note that priors are not the same as specifying an initial value for your open predicate in a data file. Once optimization starts, the initial value specified in the data file will quickly get changed and have little/no impact on the final optimization. A prior however, is a ground rule that becomes a full fledged potential function that actively participates in optimization.
Negative Priors
Negative priors are the most common type of prior in PSL. It assumes that all ground atoms for the predicate are zero.
Negative priors may be specified using logical rules:
1.0: ~Friends(A, B) ^2This prior can be interpreted as "By default, people are not friends".
Arithmetic rules may also be used to specify a negative prior:
1.0: Friends(A, B) = 0 ^2Positive Priors
Positive priors can be a little more tricky than negative priors.
If you want all the ground atoms to take the same positive prior, then you can just use an arithmetic rule:
1.0: Friends(A, B) = 0.75 ^2If you want different ground atoms to have different positive priors, then you will need to use a surrogate predicate. First, create a new closed predicate that corresponds 1-to-1 with your open predicate you wish to put the prior on. Then add observations for the surrogate predicate with the truth value being the prior you wish to put on that ground atom. Now just create a rule that directly ties together the surrogate predicate to the open predicate. See the example below.
Non-Uniform Prior Example
Consider a PSL program where we are trying to infer friendship (the Friends predicate).
We may have a prior belief on the friendship quality between all people in our data.
To encode this prior belief, we will first construct a surrogate predicate called FriendsPrior (the name does not matter).
Now we will load FriendsPrior with observations where the truth value of the observation is our prior.
Our data file for FriendsPrior may look something like:
Alice Bob 1.0
Alice Charlie 0.75
Bob Charlie 0.33Now we will add this rule that acts as our prior:
1.0: FriendsPrior(A, b) -> Friends(A, B) ^2Special Operators
Both logical and arithmetic rules support some special operators.
== (=) - Equals
Ensure that that the left and right side are equal.
Note that this is not the same as a similarity function evaluating to 1.
Two variables may be 100% similar, but equals will only evaluate to 1 unless they refer to the same value.
!= (~=) - Not Equals
Evaluates to 1 when both side are not the same.
This is a very common operator to use in most rules.
For example, consider the following two rules:
Nice(A) && Nice(B) -> Friends(A, B)
Nice(A) && Nice(B) && (A != B) -> Friends(A, B)If A and B can both take the values "Alice" and "Bob", then the first rule would generate the following groundings:
Nice("Alice") && Nice("Alice") -> Friends("Alice", "Alice")
Nice("Alice") && Nice("Bob") -> Friends("Alice", "Bob")
Nice("Bob") && Nice("Bob") -> Friends("Bob", "Bob")
Nice("Bob") && Nice("Alice") -> Friends("Bob", "Alice")While the second rule would only generate two groundings:
Nice("Alice") && Nice("Bob") -> Friends("Alice", "Bob")
Nice("Bob") && Nice("Alice") -> Friends("Bob", "Alice")% (^) - Non-Symmetric
Ensure that the reverse (or equal) paring of the two operands is not grounded.
For example, consider the following two rules:
SimilarNames(A, B) && (A % B) -> SamePerson(A, B)
SimilarNames(A, B) -> SamePerson(A, B)If A and B can both take the values "Alice" and "Bob", then the first rule would generate the following groundings:
SimilarNames("Alice", "Alice") && ("Alice" % "Alice") -> SamePerson("Alice", "Alice")
SimilarNames("Alice", "Bob") && ("Alice" % "Bob") -> SamePerson("Alice", "Bob")
SimilarNames("Bob", "Alice") && ("Bob" % "Alice") -> SamePerson("Bob", "Alice")
SimilarNames("Bob", "Bob") && ("Bob" % "Bob") -> SamePerson("Bob", "Bob")While the second rule would only generate one grounding:
SimilarNames("Alice", "Bob") && ("Alice" % "Bob") -> SamePerson("Alice", "Bob")Running a Program
To run a PSL program, change to the top-level directory of its project (the directory with the Maven pom.xml file).
Compile your project:
mvn compile
Now use Maven to generate a classpath for your project's dependencies:
mvn dependency:build-classpath -Dmdep.outputFile=classpath.out
You can now run a class with the command:
java -cp ./target/classes:`cat classpath.out` <fully qualified class name>
where \
Tips and troubleshooting
- Example programs and experiments are often deployed with a
run.shscript that will compile and run the program. Look for this script first. - The classpath for the dependencies will need to be regenerated to incorporate any new dependencies or dependencies in new locations (such as when dependency versions have been changed).
- PSL and PSL projects are configured to use the Groovy-Eclipse compiler for Maven to compile Groovy scripts. (The reference to Eclipse in its name signifies that it is based on the same compiler used in Eclipse, not that Eclipse is required.) This compiler creates regular Java class files from your Groovy scripts. The main methods generated for these class files run the scripts. Hence, the
javacommand is used to run a script.
Switching the PSL version your program uses
To change the version of PSL your project uses, edit your project's pom.xml file. The POM will declare dependencies on one or more PSL artifacts, e.g.,
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>2.0.0</version>
</dependency>
...
</dependencies>Change the version element of each such dependency to a new version (all the same one) and rebuild. See Choosing a Version of PSL to decide how to specify your version.
Using PostgreSQL with PSL
In addition to H2, PSL supports using PostgreSQL (or "Postgres" for short) as a database backend. Often the slowest operation in PSL (and all SRL systems in general) is grounding. PSL uses "bottom-up" grounding which formulates the grounding for each rule as a SQL query. This means that the choice of database backend can have large performance impacts.
Note that the Postgres backend in PSL is relatively new and may have slight changes made to its interface.
H2 vs Postgres
H2 is the default database backend for PSL. H2 is an embedded database and therefore requires no additional installation or configuration, the entire engine ships with the PSL jar. Databases are created as flat files (or fully in-memory). This makes H2 more lightweight and easy to configure. It is ideal for publishing experiments for papers that others may want to reproduce with ease. H2 will also hold information and data in memory (the same memory space that your PSL program is in). This makes certain operations fast:
- Initiating a database operation (including a query).
- Getting database/table metadata.
- Inserting data.
However, the drawback of H2 is the same as its greatest asset... simplicity. H2 has a simplified query planner, index structure, and data management. As a result, it it often slow when queries get big (lots of ground rules) and/or complicated (rules with many atoms/predicates). To counter these drawbacks, PSL also supports using a Postgres database backend.
Postgres follows the pattern of a more typical database engine where there is a service installed on some server (which may be the local machine) which accepts connections from clients. Postgres is a production-grade, open source database engine and can easily scale into terabytes (but hopefully you are working with much less data). Because Postgres is not embedded, it can be more complicated and robust. The per-query overhead is higher with Postgres (because it needs to talk to another (possibly remote) process), but the queries typically run much faster.
For simple/small queries (ones that typically run in less than 10 seconds), we typically see H2 and Postgres preforming similarly (or H2 even faster). However with larger queries, Postgres often runs 1-3 orders of magnitude faster. The more data, the greater the difference between the two. A general rule of thumb is that if you have more than 1 million groundings, consider switching to Postgres.
Installing Postgres
We recommend at least Postgres v9.5. The Postgres website has all the directions you should need for installing Postgres. If you still have issues, just try searching the internet for it. Postgres is very popular, so the internet should have a wealth of answers for you.
Setting Up The Database
Once you have Postgres installed, you need to setup a database and user.
Security Note
In this section, we will assume that your Postgres instance is only accessible to the local machine and not open to the world.
If you want to open up your database please take the time to read up on the security implications for that.
For both performance and security reasons, we strongly recommend connecting to a database that is on the same machine and that only accepts local connections.
To accept all local connections, you can setup trust-based authentication in your Client Authentication Configuration File (usually called pg_hba.conf).
Adding this line to the bottom will let all local connections to connect.
local all all trustDatabase
Creating a database in Postgres can be done with the createdb command.
You can call your database whatever you want.
createdb psl
User
Similar to creating a database, you can create a user with the createuser command.
It is easiest to create your psl user as a superuser (-s) so it can properly administrate the database.
However, people more versed in database administration can clamp down the permissions more tightly.
createuser -s jayConfiguration
To get the most performance out of our database, we typically use some additional configuration options.
These are fully optional and PSL will run fine without them.
The general themes of the options are to increase the memory, decrease durability (since we will generally not need the database after PSL completes), and force some query plans.
These options should be in your postgresql.conf file.
# shared_buffers = 1/4 of system memory
# effective_cache_size = 1/2 of system memory
# For example, on a 16GB machine:
shared_buffers = 4GB
effective_cache_size = 8GB
# No Durability
fsync = off
full_page_writes = off
synchronous_commit = off
# Query Optimization
# Disable nested loops.
enable_nestloop = off
# Limit the write-ahead log (WAL)
# max_wal_size = 1/2 of shared_buffers
max_wal_size = 2GB
wal_buffers = 32MB
wal_level = minimal
max_wal_senders = 0
checkpoint_timeout = 30Using PostgreSQL in PSL
Groovy
To use Postgres in the Groovy interface, just use the PostgreSQLDriver instead of the H2DatabaseDriver. There are various constructors that take in different information ranging from a database name to a full connection string.
DataStore dataStore = new RDBMSDataStore(new H2DatabaseDriver(Type.Disk, "/tmp/psl", true), config);DataStore dataStore = new RDBMSDataStore(new PostgreSQLDriver("psl", true), config);CLI
To use Postgres in the CLI, just use the --postgres (-p) option.
This flag has one required argument, the name of the database to connect to.
This means that currently, you must be able to connect to that database as the current user (the one invoking PSL) without a password.
java -jar psl-cli-CANARY.jar --infer --data friendship.data --model friendship.psl --postgres psl
Using the CLI
PSL provides a Command Line Interface. The CLI is the easiest interface to PSL and handles most situations where you do not need additional customization.
Setup
PSL requires that you have Java installed .
Running your first program
Let's first download the files for our example program, run it and see what it does!
In this program, we'll use information about known locations of some people, know people know, and what people like to infer who knows each other. We'll first run the program and see the output. We will be working from the command line so open up your shell or terminal.
Get the code
As with the other PSL examples, you can find all the code in our psl-examples repository.
We will be using the simple-acquaintances example.
git clone https://github.com/linqs/psl-examples.git
cd psl-examples/simple-acquaintances/cliRun your first PSL program
All the required commands are contained in the run.sh script.
However, the commands are very simple and can also be run individually.
The PSL jar will be fetched automatically. You can also select what version of PSL if fetched/used at the top of this script.
You should now see output that looks like this (note that the order of the output lines may differ):
Running PSL Inference
0 [main] INFO org.linqs.psl.cli.Launcher - Loading data
81 [main] INFO org.linqs.psl.cli.Launcher - Data loading complete
81 [main] INFO org.linqs.psl.cli.Launcher - Loading model
159 [main] INFO org.linqs.psl.cli.Launcher - Model loading complete
159 [main] INFO org.linqs.psl.cli.Launcher - Starting inference
224 [main] INFO org.linqs.psl.application.inference.MPEInference - Grounding out model.
320 [main] INFO org.linqs.psl.application.inference.MPEInference - Beginning inference.
420 [main] INFO org.linqs.psl.reasoner.admm.ADMMReasoner - Optimization completed in 404 iterations. Primal res.: 0.022839682, Dual res.: 6.607145E-4
420 [main] INFO org.linqs.psl.application.inference.MPEInference - Inference complete. Writing results to Database.
447 [main] INFO org.linqs.psl.application.inference.MPEInference - Results committed to database.
457 [main] INFO org.linqs.psl.cli.Launcher - Inference Complete
461 [main] INFO org.linqs.psl.cli.Launcher - Starting discrete evaluation
472 [main] INFO org.linqs.psl.cli.Launcher - Discrete evaluation results for KNOWS -- Accuracy: 0.5961538461538461, Error: 21.0, Positive Class Precision: 0.7333333333333333, Positive Class Recall: 0.6285714285714286, Negative Class Precision: 0.4090909090909091, Negative Class Recall: 0.5294117647058824,
472 [main] INFO org.linqs.psl.cli.Launcher - Discrete evaluation completeWhere are the prediction?
By default, the PSL examples output the results into the inferred-predicates directory.
The results for this program will looks something like:
$ cat inferred-predicates/KNOWS.txt | sort
'Alex' 'Arti' 0.9966862201690674
'Alex' 'Ben' 0.5923290848731995
'Alex' 'Dhanya' 0.48786869645118713
< ... 50 rows omitted for brevity ...>
'Steve' 'Elena' 0.49548637866973877
'Steve' 'Jay' 0.614285409450531
'Steve' 'Sabina' 0.5133784413337708What did it do?
Now that we've run our first program that performs link prediction to infer who knows who, let's understand the steps that we went through to infer the unknown values: defining the underlying model, providing data to the model, and running inference to classify the unknown values.
Defining a Model
A model in PSL is a set of logic-like rules.
The model is defined inside a text file with the format .psl. We describe this model in the file simple-acquaintances.psl.
Let's have a look at the rules that make up our model:
20: Lived(P1, L) & Lived(P2, L) & (P1 != P2) -> Knows(P1, P2) ^2
5: Lived(P1, L1) & Lived(P2, L2) & (P1 != P2) & (L1 != L2) -> !Knows(P1, P2) ^2
10: Likes(P1, L) & Likes(P2, L) & (P1 != P2) -> Knows(P1, P2) ^2
5: Knows(P1, P2) & Knows(P2, P3) & (P1 != P3) -> Knows(P1, P3) ^2
Knows(P1, P2) = Knows(P2, P1) .
5: !Knows(P1, P2) ^2The model is expressing the intuition that people who have lived in the same location or like the same thing may know each other.
The integer values at the beginning of rules indicate the weight of the rule.
Intuitively, this tells us the relative importance of satisfying this rule compared to the other rules.
The ^2 at the end of the rules indicates that the hinge-loss functions based on groundings of these rules are squared, for a smoother tradeoff.
For a full description of rule syntax, see the Rule Specification .
For more details on hinge-loss functions and squared potentials, see the publications on our PSL webpage.
Loading the Data
PSL rules consist of predicates. The names of the predicates used in our model and possible substitutions of these predicates with actual entities from our network are defined inside the file simple-acquaintances.data.
Let's have a look:
predicates:
Knows/2: open
Likes/2: closed
Lived/2: closed
observations:
Knows : ../data/knows_obs.txt
Lived : ../data/lived_obs.txt
Likes : ../data/likes_obs.txt
targets:
Knows : ../data/knows_targets.txt
truth:
Knows : ../data/knows_truth.txtIn the predicate section, we list all the predicates that will be used in rules that define the model.
The keyword open indicates that we want to infer some substitutions of this predicate while closed indicates that this predicate is fully observed.
I.e. all substitutions of this predicate have known values and will behave as evidence for inference.
For our simple example, we fully observe where people have lived and what things they like (or dislike).
Thus, Likes and Lived are both closed predicates.
We are aware of some instances of people knowing each other, but wish to infer the other instances Knows an open predicate.
In the observations section, for each predicate for which we have observations, we specify the name of the tab-separated file containing the observations.
For example, knows_obs.txt and lived_obs.txt specifies which people know each other and where some of these people live, respectively.
The targets section specifies a .txt file that, for each open predicate, lists all substitutions of that predicate that we wish to infer.
In knows_targets.txt, we specify the pairs of people for whom we wish to infer.
The truth section specifies a .txt file that provides a set of ground truth observations for each open predicate.
Here, we give the actual values for the Knows predicate for all the people in the network as training labels. We describe the the general data loading scheme in more detail in the sections below.
More advanced features of the .data file can be found on the CLI Data File Format page.
Writing PSL Rules
To create a PSL model, you should define a set of rules in a .psl file.
Let's go over the basic syntax to write rules. Consider this very general rule form:
w: P(A,B) & Q(B,C) -> R(A,C) ^2The first part of the rule, w, is an integer value that specifies the weight of the rule.
In this example, P, Q and R are predicates.
Logical rules consist of the rule "body" and rule "head."
The body of the rule appears before the -> which denotes logical implication.
The body can have one or more predicates conjuncted together with the & that denotes logical conjunctions.
The head of the rule should be a single predicate.
The predicates that appear in the body and head can be any combination of open and closed predicate types.
The Rule Specification page contains the full syntax for PSL rules.
Organizing your Data
In a .data file, you should first define your predicates: as shown in the above example.
Use the open and closed keywords to characterize each predicate.
A closed predicate is a predicate whose values are always observed.
For example, the knows predicate from the simple example is closed because we fully observe the entire network of people that know one another.
On the other hand, an open predicate is a predicate where some values may be observed, but some values are missing and thus, need to be inferred.
As shown above, then create your observations:, targets: and truth: sections that list the names of files that specify the observed values for predicates, values you want to infer for open predicates, and observed ground truth values for open predicates.
For all predicates, all possible substitutions should be specified either in the target files or in the observation files. The observations files should contain the known values for all closed predicates and can contain some of the known values for the open predicates. The target files tell PSL which substitutions of the open predicates it needs to infer. Target files cannot be specified for closed predicates as they are fully observed.
The truth files provide training labels in order learn the weights of the rules directly from data. This is similar to learning the weights of coefficients in a logistic regression model from training data.
Running Inference
Run inference with the general command:
java -jar psl-cli.jar --infer --model [name of model file].psl --data [name of data file].data
When we run inference, the inferred values are outputted to the screen. If you want to write the outputs to a file and use the inferred values in various ways downstream, you can use:
java -jar psl-cli.jar --infer --model [name of model file].psl --data [name of data file].data --output [directory to write output files]
Values for all predicates will be output as tab-separated files in the specified output directory.
With the inferred values, some downstream tasks that you can perform are:
- if you have a gold standard set of labels, you can evaluate your model by computing standard metrics like accuracy, AUC, F1, etc.
- you may want to use the predicted outputs of PSL as inputs for another model.
- you may want to visualize the predicted values and use the outputs of PSL as inputs to a data visualization program.
Using the Groovy Interface
Setup
Ensure that you have the prerequisites installed.
Examples
Looking at the examples is a great way to get familiar with the Groovy interface. We also have an in depth walkthrough of one of our examples.
Project Setup
After you have looked at the examples, you should set up a new PSL project . You can run a PSL Groovy program in the same way that you run an example program.
Groovy Specifics
Here are some more detailed topics that you may need:
Version Cheatsheet
| Release Date | PSL | PSL Utils | PSL Experimental | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2015-10-11 | 1.2.1 | Code | API Doc | Static Wiki | ||||||
| 2017-07-04 | 2.0.0 | Code | API Doc | Static Wiki | 1.0.0 | Code | API Doc | 1.0.0 | Code | API Doc |
| 2018-07-31 | 2.1.0 | Code | API Doc | Static Wiki | 2.1.0 | Code | API Doc | 2.1.0 | Code | API Doc |
Working With Canary
What is Canary?
The Canary is a published build of PSL that is based on the development branch. The name "Canary" comes from the iconic use of a canary in a coal mine to detect toxic gas. The build is somewhere near the tip of the development tree. It is updated whenever the PSL developers feel a significant change has been made in development.
Versioned vs Unversioned Canary
To make using the canary build easier for PSL users, we release two versions of the canary build in parallel.
On version is always called CANARY and will replace the previous build.
The other version will be called CANARY-X.Y.Z where X.Y matches the major/minor number of the next stable release and Z just increments by one for each canary build.
Unfortunately, we do not yet have any fancy infrastructure to check what canary versions are available, so the easiest way will be to just look at the maven repository.
If you always want the latest and are willing to have potential incompatibilities between updates, use the unversioned canary. If you want a newer version but don't want it to update or you are collaborating with other people, use the versioned canary.
Using Canary
Groovy
The use canary, simply change your PSL version in your pom.xml to CANARY or CANARY-X.Y.Z (with the proper substitution for X.Y.Z).
<dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>CANARY</version>
</dependency>
...
</dependencies><dependencies>
...
<dependency>
<groupId>org.linqs</groupId>
<artifactId>psl-groovy</artifactId>
<version>CANARY-2.1.0</version>
</dependency>
...
</dependencies>CLI
Using the canary in the CLI just means grabbing the new jar file from the Maven repository.
How do I update my Canary?
If you are using the versioned canary, then just update your version numbers in your pom.
If you are using the unversioned canary, then you will have to delete the old canary from your Maven cache.
On Lunix/Mac, this is at: ~/.m2/repository/org/linqs/psl*/CANARY